Rheology is the study of the deformation and flow of matter, distinguishing between Newtonian and non-Newtonian fluids based on their viscosity behavior. Key concepts include:
- Newtonian Fluids: Follow Newton’s law, where stress is proportional to strain rate with a constant viscosity.
- Non-Newtonian Fluids: Viscosity depends on strain rate, leading to complex flow behaviors.
- Examples of Non-Newtonian Fluids: Polymer solutions, thermoplastics, drilling fluids, paints, fresh concrete, and biological fluids.
- Key Properties of Non-Newtonian Fluids:
- Normal-Stress Differences: Unique stress distributions not present in Newtonian fluids.
- Shear-Thickening: Viscosity increases with strain rate.
- Shear-Thinning: Viscosity decreases with strain rate.
- Thixotropy: Viscosity decreases over time under constant shear.
- Rheopexy: Viscosity increases over time under constant shear.
- Extrudate Swell: Expansion of material upon exiting a die.
These properties lead to diverse applications and challenges in material processing and fluid mechanics.
Characterization of normal stress differences for viscoelastic solids
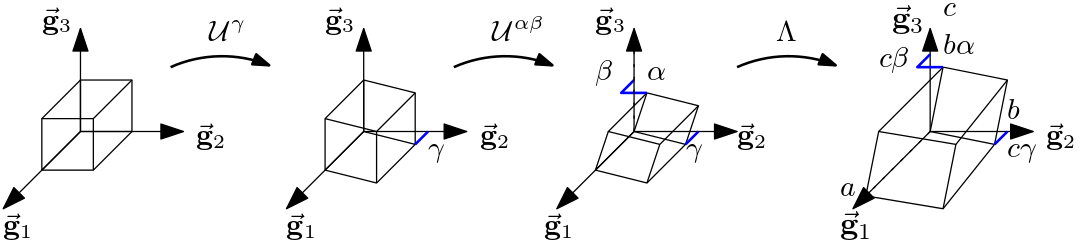
In standard rheometry, measuring normal-stress differences requires both parallel plate and cone-and-plate rheometers. However, for viscoelastic solids, this approach faces limitations. This paper presents an alternative method using matrix decomposition techniques. Key points:
- Standard Rheometry Setup: Normal-stress differences are typically measured using a parallel plate rheometer alongside a cone-and-plate rheometer.
- Cone-and-Plate Advantage: Ensures a constant state of stress at the cone surface, allowing for accurate stress measurements.
- Challenge with Soft Solids: Viscoelastic solids cannot be tested using a cone-and-plate setup, preventing precise normal-stress difference measurements.
- Proposed Solution: The study introduces an alternative method using Gram-Schmidt or QR decomposition of the deformation gradient to calculate normal-stress differences.
Thixotropic behavior of parafin/wax suspensions.
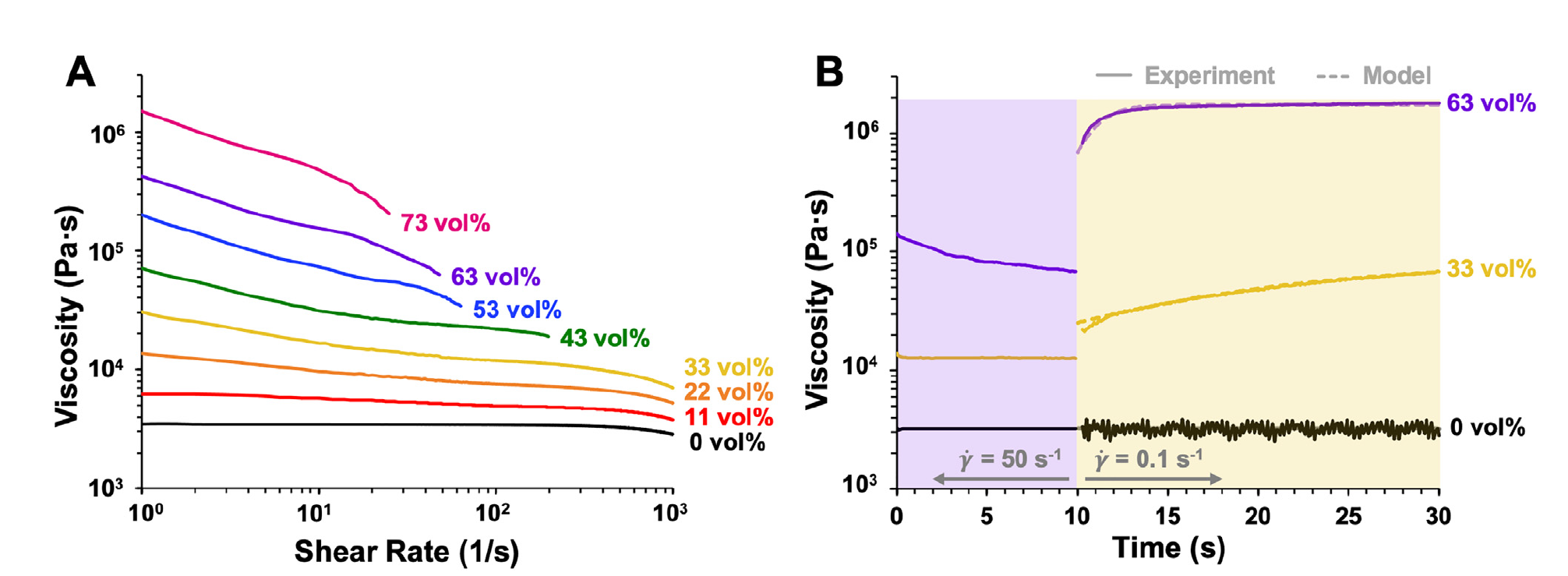
Rheological Considerations in Direct Ink Writing of Functional Composites
- Importance of 3D Printing (3DP) for Functional Materials
- Enables complex/custom geometries and gradient properties.
- Direct Ink Writing (DIW) as a Common 3DP Technique
- Utilizes particle-filled fluid matrices as printable inks.
- Solid particles act as both rheology modifiers and functional fillers.
- Need for a Comprehensive Rheological Description
- Filler loading impacts viscosity, influencing printability.
- Existing models describe polymeric systems but lack specificity for 3D-printable composites.
- Improved rheological understanding will accelerate new material development.
Energy dissipation in phase change salogels
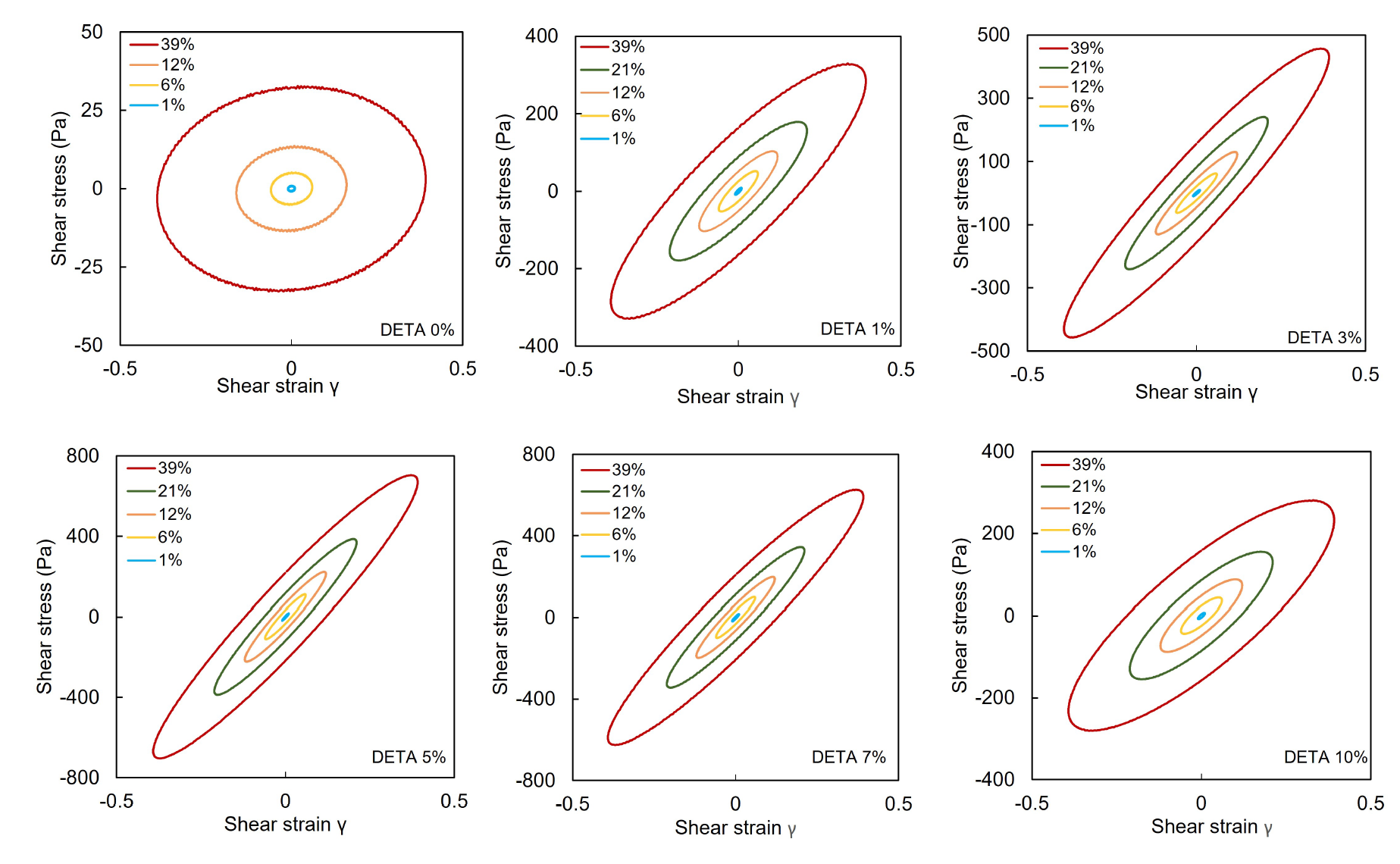 Phase change salogels are physical networks designed to shape-stabilize salt hydrate phase change materials (PCMs) and prevent molten PCM leakage. Below are the key points summarizing the study:
Phase change salogels are physical networks designed to shape-stabilize salt hydrate phase change materials (PCMs) and prevent molten PCM leakage. Below are the key points summarizing the study:
- Salogel Mechanics: Unlike chemically crosslinked gels, salogels restructure dynamically by breaking and reforming physical bonds, making them effective at dissipating energy under deformation.
- Crosslinker Influence: Different concentrations of diethylenetriamine (physical crosslinker) were incorporated into a fixed concentration of polyvinyl alcohol (PVA) within a high-salinity lithium nitrate trihydrate PCM.
- Viscoelastic Characterization: The network’s viscoelasticity was analyzed through oscillatory rheology.
- Energy Dissipation Measurement: Dissipated energy was quantified by calculating the enclosed area in Lissajous stress-strain curves at varying strain amplitudes and a constant frequency of 1 rad/s.
This study explores how physical crosslinking affects salogel viscoelasticity and energy dissipation, which are critical for PCM stabilization.
Relevant Publications
- Cipriani, Ciera E., Yalan Shu, Emily B. Pentzer, and Chandler C. Benjamin. “Viscoelastic and thixotropic characterization of paraffin/photopolymer composites for extrusion-based printing.” Physics of Fluids 34, no. 9 (2022): 093106.
- Karimineghlani, Parvin, Abdelrahman A. Youssef, and Chandler C. Benjamin. “Energy dissipation in phase change salogels under shear stress.” Polymer (2022): 124977.
- Cipriani, Ciera E., Taekwang Ha, Oliver B. Martinez Defilló, Manoj Myneni, Yifei Wang, Chandler C. Benjamin, Jyhwen Wang, Emily B. Pentzer, and Peiran Wei. “Structure–processing–property relationships of 3D printed porous polymeric materials.” ACS Materials Au 1, no. 1 (2021): 69-80.
- Paul, Sandipan, Alan D. Freed, and Chandler C. Benjamin. “Application of the Gram–Schmidt factorization of the deformation gradient to a cone and plate rheometer.” Physics of Fluids 33.1 (2021): 017113.
Publications by Collaborators
- Paul, Sandipan, and Alan D. Freed. “A simple and practical representation of compatibility condition derived using a QR decomposition of the deformation gradient.” Acta Mechanica 231 (2020): 3289-3304.
- Paul, Sandipan, and Alan D. Freed. “Characterizing geometrically necessary dislocations using an elastic–plastic decomposition of Laplace stretch.” Zeitschrift für angewandte Mathematik und Physik 71.6 (2020): 1-22.
